Параллельный перенос вектора. Критика | страница 4
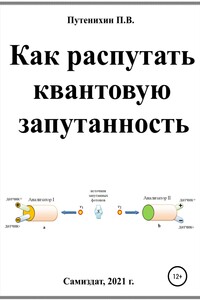
"На рисунке начальное положение вектора обозначено цифрой 1 (северный полюс). Он обносится параллельным образом (положения 2, 3, …) вокруг сферического треугольника, все углы которого равны 90>o. По возвращении в исходную точку вектор (положение 4) оказывается повернутым на 90>o:
(положительна; направление поворота совпадает с направлением обхода) [8, т.1, с.412]".
Рис.1. Паралельный перенос вектора [8, т.1, с.412]
Гауссова кривизна γ>G в рассмотренном случае сферической поверхности определена как отношение площади, обойденной вектором, к углу поворота вектора, когда он вернулся в исходную точку [8, т.1, с.412]. В примере с треугольным контуром, действительно, получается вполне осмысленная величина кривизны – 1/a>2, где а – радиус сферы:
Как видим, и в этом случае при обходе по замкнутому контуру результирующий вектор не совпал по направлению с исходным. Хотя на рисунке это не очень заметно, но в предпоследней точке 3 направление вектора в точности совпадает с последним направлением 4 при обходе треугольника. Тем не менее, и в данном случае возникает вопрос по изображению векторов. Судя по всему, векторы в точках 2 и 3 направлены точно по сторонам треугольника, то есть, по определению параллельны друг другу. Однако они изображены слишком короткими отрезками, поэтому на рисунке не совсем ясно, лежат ли они на поверхности сферы? На плоском пространстве поверхности сферы возможны лишь векторы, полностью совпадающие с этой поверхностью.
В случае сферического треугольника вектор, как показано на рисунке, при переносе изменил своё направление. Но что будет, если взять квадратный или прямоугольный контур? Как видно на рис.2а при таком переносе итоговый угол φ = 0, поэтому кривизна оказывается равной нулю. Получается, что метод не вполне корректен, поскольку даёт для одной и той же поверхности при использовании одного и того же правила разные значения.
Немного доработаем рисунок, чтобы устранить эту неопределенность с направлениями вектора. Будем считать, что исходный вектор 1, векторы 2, 3 и 4 касательны к дугам 1-2 и 3-4, то есть, к боковым сторонам треугольника, вдоль которого они переносятся. Именно это и означает их параллельность.
Поскольку мы вправе произвести параллельный перенос вектора по произвольному маршруту, то мы добавим ещё один отрезок, превратив сферический треугольник в сферический квадрат (вернее, криволинейный четырехугольник). И сразу же обнаруживаем, что наш вопрос возник, вообще-то, не на пустом месте. Мы видим два переноса вектора по ортогональным к меридианам линиям – 2-3 и 4-1. Вновь возникает вопрос: почему при переносе по параллели 2-3 вектор остался коллинеарным своим меридианам 1-2 и 3-4, а на отрезке 4-1 нет? Логического оправдания такого различия, похоже, не существует.